I wanted to get back to the analysis of quotes from a semantics perspective and write about searching & clustering them with Latent Semantic Analysis (LSA). Thought it was going to be a straightforward exercise in applying the venerable gensim package and appreciating the augmented information retrieval capabilities of LSA on top of regular keyword based searches. But it was not to be. I kept running into strange issues that I could not quite make sense of from what I understood LSA to have brought to the table. The search results and clustering thereof seemed sensitive to the subset of quotes I chose to work with in building the concept space.
I needed to dig deeper into what exactly LSA was doing. LSA is basically Singular Value Decomposition (SVD) applied to the term-document matrix. Unfortunately SVD is not intuitive – especially if you have been a bit out of touch with it for a while as I have been. But SVD is basically a more general form of Principal Component Analysis (PCA) that is widely used in statistical analysis 1. Idealized tests with PCA showed similar sensitivity as well that I decided to focus on a short summary of that here and get to LSA in a later one – hopefully with a better understanding as to how to interpret the results.
1. Data dimensionality
In any experiment or a data collection exercise there is some choice on choosing what aspects or characteristics of the process we measure to describe this process. Clearly we would like to be able to describe/model the process with the fewest number of observations and using the fewest number of characteristics. But with no a-priori knowledge of the underlying model we have to pick some characteristics of the process that we think are the driving factors, and of course those that we can actually measure.
The dimensionality of a data set can be loosely defined as the number of independent variables required to satisfactorily describe the entire data set. Say we measure 5 characteristics (variables) in an experiment and later find in the analysis that there are 2 constraints among these 5 variables. The dimensionality of the data set is simply 3 ( = 5 – 2). Had we known prior to the experiment that these constraints/relationships existed – we could 2 have saved some work by making fewer measurements on fewer variables.
Principal Component Analysis (PCA) and more generally Singular Value Decomposition (SVD) are widely used techniques in data analysis for discovering potential relations in multi dimensional data, and thereby allowing for a reduction in the dimensionality of the model required to describe the system. But, while any functional relation such as ![]() is sufficient for dimensionality reduction, PCA can only find linear relationships if they exist. For example, if the 2 constraints among the 5 variables above, are nonlinear – PCA can still claim that the data has 3, 4 or 5 dimensions, depending on which sample of the data is used. This is perhaps elementary as nobody would knowingly apply PCA to nonlinear data. But it can happen when we are exploring the data, do not have prior insight into the nonlinearity of the model, and of course when we use tools that may have builtin linearity assumptions.
is sufficient for dimensionality reduction, PCA can only find linear relationships if they exist. For example, if the 2 constraints among the 5 variables above, are nonlinear – PCA can still claim that the data has 3, 4 or 5 dimensions, depending on which sample of the data is used. This is perhaps elementary as nobody would knowingly apply PCA to nonlinear data. But it can happen when we are exploring the data, do not have prior insight into the nonlinearity of the model, and of course when we use tools that may have builtin linearity assumptions.
2. Correlations and dimensionality reduction
Consider an experiment where we have n measurements of 2 variables X and Y. We will use PCA to discover if the data is really 2-dimensional or could just be described with a single variable. Our data is synthetic with X and Y centered around the origin ![]() (so we can directly apply PCA on it), i.e.,
(so we can directly apply PCA on it), i.e.,
![Rendered by QuickLaTeX.com \[ \sum\limits_{i=1}^{n} X_i = 0 \qquad \sum\limits_{i=1}^{n} Y_i = 0 \]](https://xplordat.com/wp-content/ql-cache/quicklatex.com-cacfa0cf13e09fc9a91336e8cfdd86d8_l3.png)
and having an approximate functional relationship that we hope to ‘discover’ with PCA so we confirm PCA is working correctly for us. ![]() and
and ![]() yield a
yield a ![]() data matrix B, and a
data matrix B, and a ![]() covariance matrix C:
covariance matrix C:
![Rendered by QuickLaTeX.com \[ B = \begin{bmatrix} X_1 & Y_1 \\ X_2 & Y_2 \\ X_3 & Y_3 \\ \hdotsfor{2} \\ X_n & Y_n\end{bmatrix} \qquad C = \frac {B^T \cdot B}{n-1} = \frac{1}{n-1} \begin{bmatrix} \sum\limits_{i=1}^n X_i^2 & \sum\limits_i^n X_i Y_i \\ \sum\limits_{i=1}^n X_i Y_i & \sum\limits_{i=1}^n Y_i^2 \end{bmatrix} \]](https://xplordat.com/wp-content/ql-cache/quicklatex.com-9232b29474ad85218488c85148a90246_l3.png)
2.1 A linear correlation between X and Y
Let ![]() , where
, where ![]() . The covariance matrix would be:
. The covariance matrix would be:
![Rendered by QuickLaTeX.com \[ C_1 = \sum\limits_{i=1}^n X_i^2 \begin{bmatrix} 1 & a \\ a & a^2 \end{bmatrix} \]](https://xplordat.com/wp-content/ql-cache/quicklatex.com-f6a72dc62ecefd655b63d23e985de8b7_l3.png)
Since our measurements are NOT all at ![]() . So we can readily compute the 2 eigenvalues
. So we can readily compute the 2 eigenvalues ![]() and
and ![]() and the associated eigenvectors
and the associated eigenvectors ![]() and
and ![]() for the symmetric matrix
for the symmetric matrix ![]() .
.
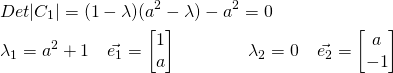
The only dominant eigenvalue here is ![]() , with the associated eigenvector
, with the associated eigenvector ![]() – that aligns perfectly with the line
– that aligns perfectly with the line ![]() .
.
We can also estimate ![]() via a Least Squares fit for the same data with the function
via a Least Squares fit for the same data with the function ![]() as
as ![]() which minimizes
which minimizes ![]() . We get:
. We get:
![Rendered by QuickLaTeX.com \[ \frac{dS}{d\hat{a}} = \sum\limits_{i=1}^{n} 2 X_i (\hat{a} X_i - Y_i) = 0 \qquad => \hat{a} = \frac{1}{\sum\limits_{i=1}^{n} X_i^2} \sum\limits_{i=1}^{n} X_i Y_i \]](https://xplordat.com/wp-content/ql-cache/quicklatex.com-097ef7e2ebe0c1df887c27dade06b07d_l3.png)
When ![]() we can verify from above that least squares fit correctly gives
we can verify from above that least squares fit correctly gives ![]() . Thus both PCA and a least squares approach successfully identify the only known relationship in our synthetic data and correctly reduce the dimensionality to 1 from 2 – irrespective of
. Thus both PCA and a least squares approach successfully identify the only known relationship in our synthetic data and correctly reduce the dimensionality to 1 from 2 – irrespective of ![]() , i.e. irrespective of where we chose to measure.
, i.e. irrespective of where we chose to measure.
2.2 A nonlinear correlation between X and Y
Let ![]() . For sampling we choose
. For sampling we choose ![]() to be symmetrically distributed around
to be symmetrically distributed around ![]() , so our synthetic data for
, so our synthetic data for ![]() will automatically obey
will automatically obey ![]() . For more extreme nonlinear behavior around the origin (and concurrent effects on dimensionality as measured by PCA), we can use circles or ellipses, but the algebra will get uglier. We can make our point clear enough with
. For more extreme nonlinear behavior around the origin (and concurrent effects on dimensionality as measured by PCA), we can use circles or ellipses, but the algebra will get uglier. We can make our point clear enough with ![]() . The covariance matrix
. The covariance matrix ![]() would be:
would be:
![Rendered by QuickLaTeX.com \[ C_2 = \begin{bmatrix} \sum\limits_{i=1}^n X_i^2 & a \sum\limits_{i=1}^n X_i^4 \\ a \sum\limits_{i=1}^n X_i^4 & a^2 \sum\limits_{i=1}^n X_i^6 \end{bmatrix} \]](https://xplordat.com/wp-content/ql-cache/quicklatex.com-15f37f5d04e2f917556f8373d52dd81b_l3.png)
Unlike for the linear case, the eigenvalues & eigenvectors are now a function of the measurements. Plugging some numbers into ![]() and
and ![]() we can compute the eigenvalues
we can compute the eigenvalues ![]() ,
, ![]() and in particular the ratio
and in particular the ratio ![]() . If it is small enough we can ignore the second dimension (i.e. the eigenvector
. If it is small enough we can ignore the second dimension (i.e. the eigenvector ![]() associated with
associated with ![]() ) and choose to describe the overall process with one variable
) and choose to describe the overall process with one variable ![]() – that is a linear combination of
– that is a linear combination of ![]() and
and ![]() . Clearly this decision to treat the model as 1-dimensional or 2-dimensional is a function of our choice for
. Clearly this decision to treat the model as 1-dimensional or 2-dimensional is a function of our choice for ![]() and also the threshold used to ignore the contribution from
and also the threshold used to ignore the contribution from ![]() .
.
As for least squares, we can again fit the data to ![]() and find
and find ![]() with:
with:
![Rendered by QuickLaTeX.com \[ \frac{dS}{d\hat{a}} = \sum\limits_{i=1}^{n} 2 X_i^3 (\hat{a} X_i^3 - Y_i) = 0 \qquad => \hat{a} = \frac{1}{\sum\limits_{i=1}^{n} X_i^6} \sum\limits_{i=1}^{n} X_i^3 Y_i \]](https://xplordat.com/wp-content/ql-cache/quicklatex.com-d1f64e7eb074ec5db76a9e8b05a48858_l3.png)
When the relationship is exact, i.e. ![]() , we can verify from above that least squares fit correctly gives
, we can verify from above that least squares fit correctly gives ![]() – irrespective of the choice of
– irrespective of the choice of ![]() . The point here is NOT to compare PCA with least squares. The whole reason we bring least squares into the picture here is to show that the model/data and sampling strategy are not pathologically flawed, and work perfectly fine – when analysed with the right tool. Attempting to use PCA to reduce the dimensionality of a nonlinear data set was our mistake.
. The point here is NOT to compare PCA with least squares. The whole reason we bring least squares into the picture here is to show that the model/data and sampling strategy are not pathologically flawed, and work perfectly fine – when analysed with the right tool. Attempting to use PCA to reduce the dimensionality of a nonlinear data set was our mistake.
3. Conclusion
The fact that the number of independent dimensions as predicted by PCA can change based on the data points used, could be a clue that we are dealing with nonlinear relationships among our variables in the data. In the toy example here we can instead work with ![]() and
and ![]() as our new variables as
as our new variables as ![]() – a linear relationship. This is in general not possible and nonlinear dimensionality reduction approaches like Kernel PCA could be the answer if that is the objective. Our interest here of course is on document search/clustering with LSA and what the take away would be from the analysis here as LSA is anchored on SVD.
– a linear relationship. This is in general not possible and nonlinear dimensionality reduction approaches like Kernel PCA could be the answer if that is the objective. Our interest here of course is on document search/clustering with LSA and what the take away would be from the analysis here as LSA is anchored on SVD.
LSA attempts to identify a set3 of hidden concepts that can be used to express both the terms & documents as linear combinations of these concepts. To the extent that it succeeds, a reduction in the dimensionality of the term-document data set is achieved. Depending on how volatile the document repo or the search index is, there will be a need to re-assess the concept space dimensionality and rebuild it on a periodic basis.
- see the following references for example – Gilbert Strang, Jonathon Shlens, Jeremy Kun, Alex Tomo etc…
- I say ‘could’ because there are limitations on what we can actually ‘measure’ in an experiment. Just because the analysis shows that the results are a function of the compound variable
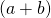 there may not be a way to measure the sum of the two variables
there may not be a way to measure the sum of the two variables  and
and 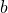 directly in the experiment
directly in the experiment - hopefully a small set, much less than the number of terms and documents in the repo