Clustering Text with Transformed Document Vectors

A sister task to classification in machine learning is clustering. While classification requires up-front labeling of training data with class information, clustering is unsupervised. There is a large benefit to unattended grouping of text on disk and we would like to know if word-embeddings can help. In fact, once identified, these clusters can then go on to serve as target classification buckets for similar future incoming text. If we succeed in this we would have obviated the need for up-front labeling! Worthy goal but more on that later.

Word-embeddings yield a linear transformation of n-long (n being the size of the vocabulary making up the text corpus) sparse document vectors to p-long dense vectors, with p << n. In the context of classification of document vectors we concluded that using tf-idf vectors with naive bayes classifier is a great starting point. While we cannot generalize, replacing words with pre-trained/custom-derived numerical vectors did not seem to do much for the classification quality. The general objective of this post (and the upcoming one) is to repeat that exercise for a clustering task. In this post we focus on the following.

Compare and contrast the distance/similarity measures for documents
How transformations can affect the clusterability of vectors
How to compare different transformations for their effectiveness at clustering.

1. Clustering Vs Classification of Documents

Clustering hinges on the notion of distance between objects, while classification hinges on the similarity of objects. The objects here are documents represented as numerical vectors as per the tested and tried bag-of-words approach and its variations (including word-embeddings). We might choose to use the euclidean distance measure for clustering and cosine similarity for classification. Intuitively we expect similar documents to be close to each other – distance wise. But that is not guaranteed unless we explicitly require it in the implementation. Things that we did not have to worry about while classifying document vectors, matter for the clustering task. Some of those would be as follows.

In any given space, length normalization is important for clustering document vectors, but not for classifying them
Distances and similarities in different transformed spaces cannot be directly compared magnitude wise to draw any conclusions
Transformations need not preserve either distances or similarities and we actually hope they change them for the better, as there would be no point otherwise in applying transformations in the first place.

Let us look at each of these in some detail focusing mainly on the distance between vectors.

2. Length Normalization

The core assumption of the vector space model for documents is that if two documents contain the same words with the same relative frequencies, then they are likely talking about the same thing. Thus the vectors built on that premise reflect it by yielding a cosine similarity of unity. We want the same end result in the clustering exercise as well. That is, we want to build clusters of documents, where the documents in each cluster are more similar to each other than they are to documents in other clusters. Makes sense right?

But clustering is in general based on distance between vectors in the feature space and not on their cosine similarity. Perhaps we could use cosine similarity itself as the distance measure. Most implementations for K-means clustering (for example scikit-learn) do not allow for a custom distance function. So if we want to use K-means implementation in scikit for clustering documents, we need the distance measure for documents to behave the same way as their cosine similarity does, to get good results for clustering documents. Cosine similarity is unaffected by the magnitude of the vectors while the distance between them is. So we require that all the document vectors be normalized to have the same length prior to a clustering task.

For illustration, consider the vectors OP, OA, OB, and OQ in Figure 1 below. OA is simply OP but with a larger magnitude. Likewise OB is a larger version of OQ. But the angle between OA, OB and that between OP and OQ is the same, and hence their cosine similarity is unaffected.

Figure 1. (A) Magnitude of vectors affects their difference but not their cosine similarity. So we need to normalize document vectors for clustering (B) Linear transformation of vectors does not in general preserve angles or lengths. So once again the document vectors should be normalized after a transformation if clustering is the objective.

(1) $\begin{align*} & \cos(\theta) = \frac{\overline{OA} \, \cdot \, \overline{OB}}{\mid \overline{OA} \mid \,\, \mid \overline{OB} \mid} = \frac{\overline{OP} \, \cdot \, \overline{OQ}}{\mid \overline{OP} \mid \,\, \mid \overline{OQ} \mid} \\ & \mid \overline{OA} - \overline{OB} \mid \, \, > \mid \overline{OP} - \overline{OQ} \mid \end{align*}$

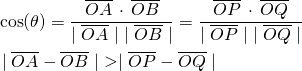
Let us be very clear that we are requiring length normalization in the context of clustering document vectors where we want the distance measure to behave like the cosine similarity measure… Length normalization is not a blanket recommendation for clustering any set of vectors… In fact it would ruin the perfect clusters we obtained in the previous post where distances needed to be well distances between the original vectors…

3. Transformations

Consider two vectors X and Y of length n, the size of the vocabulary. We transform them into shorter p-dimensional vectors X‘ and Y‘ by use of word-embeddings. We know (see for example Word Embeddings and Document Vectors: Part 2. Classification) that the transformation is linear with X’ = WX and Y’ = WY where W is the pxn matrix where p is the length of the word vectors. The cosine similarities and the distances in the new space can be derived as follows.

(2) $\begin{align*} & \cos(\theta) = \frac{X \cdot Y}{\mid X \mid \,\, \mid Y \mid} = \frac{X^T \, Y}{\mid X \mid \, \, \mid Y \mid} = \frac{X^T \, Y}{\sqrt{( X^T X ) \, (Y^T Y)} } \\ & \cos(\theta') = \frac{X' \cdot Y'}{\mid X' \mid \,\, \mid Y' \mid} = \frac{X^T \, W^T \, W \, Y}{\sqrt{ ( (WX)^T . (WX) ) \, ( (WY)^T (WY))}} = \frac{X^T \, W^T \, W \, Y}{ \sqrt{ (X^T W^T W X) (Y^T W^T W Y)}} \\ & \mid X' - Y' \mid = \mid W (X - Y) \mid = \sqrt{(X-Y)^T W^T W (X-Y)} \end{align*}$

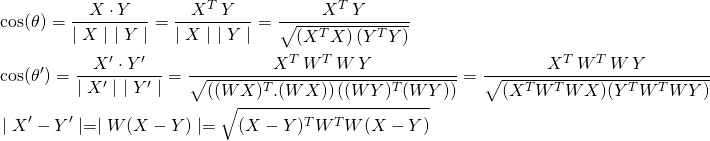
Clearly, the angles and distances between vectors in p-space are a function of W. And they would be invariant if and only if W is orthonormal.

(3) $\begin{equation*} \theta = \theta' \quad \text{and } \mid X' - Y' \mid = \mid X - Y \mid \quad \quad \text{If and only if } W^T W = I \end{equation*}$

But there is no reason to expect W to be orthonormal, as the word-vectors are derived from digesting text in a variety of ways depending on the underlying algorithm and with no requirement that they be orthonormal. As we are dealing with documents here, it follows from the argument in section 1 that we need to,

normalize the length of transformed document vectors before proceeding with a clustering task

4. Distance Measures

We are hoping that a linear transformation of vectors will enable us to better decipher the latent clusters in the data. Each transformation takes the document vectors to a different space. While we can compare distances with-in a single space, we cannot compare them across spaces. See the Figure 2 below where the clustered data in 2A got transformed via linear transformations W₁ and W₂ to produce the clusters we see in 2B and 2C respectively.

Figure 2. The relative changes in inter/intra cluster distances are the key. W₂ is a preferable transformation than W₁ even while it reduces the intercluster separation in absolute terms. The ratio inter/intra cluster distances is larger with W₂

Figure 2B shows larger absolute values for the distances separating the clusters. But Figure 2C demarcates the clusters better. The reason is clear. In Figure 2B both the intracluster and intercluster distances got larger. In Figure 2C while the overall distances got squished, the intracluster distances got squished more than the intercluster distances. That is the key. To get better delineation between the clusters we need the individual clusters as compact as possible, while being as far as possible from the other clusters. Common sense right? We can somewhat formalize this by saying

we should prefer a linear transformation that increases the ratio of intercluster distances to intracluster distances… in fact we should expect the transformation that yields the highest ratios to show best results for the clustering task

As there are many inter & intra cluster distances, here is a plausible procedure to compare different order reducing linear transformations for the clustering task.

Pick a transformation
For each cluster C_i find the median distance of its members from its centroid. Compute the average of these medians. This is a ‘representative’ distance measure for this coordinate system.
Divide each intercluster distance with this representative distance measure from 1. Find the average of these ratios.
Repeat 1-3 for each transformation. The transformation that yields large values in 3 should be better at the clustering task

5. An Example

We conclude the post with an example that solidifies our observations from the earlier sections. Consider a 2-d feature space with identifiable clusters shown in Figure 3A below. The code for reproducing these results can be downloaded from github.

Figure 3. Cluster detection with transformed vectors. The ratio of intercluster to intracluster distance measures is the metric to evaluate and compare across transformations. (A) Original vectors that show two clusters. (B) The clusters are better separated than in A (C) The transformation did not help with improving cluster detection here (D-E) Distribution of intracluster distances upon transformation. The whiskers are at 5 and 95 percentile values. The intracluster cluster distances got blown up in 3E as expected from 3B. The intracluster distances got squished in 3D agreeing with 3C.

Applying a sample linear transformation to this data we get the clusters shown in Figure 3B. The observed orthogonality in Figure 3B is not surprising because ‘we cheated’ and picked a linear transformation that aligns somewhat with the dominant directions of these clusters in Figure 3A. We do not have that luxury in general but this is just for magnifying the impact of transformations on cluster detection. Applying a diffrent random transformation yields the squished clusters shown in Figure 3C. The actual distribution of intracluster distances (from the centroid of the cluster) have changed upon these transformations. The squishing of distances in 3C/3D and expansion of distances in 3B/3E is evident.

Clearly the clusters obtained in Figure 3B are better separated than those in Figures 3A or 3C. The ratio of intercluster distance to the averaged median intracluster distances has the highest value as well for Figure 3B. That is the point we were building towards to in sections 2 thru 4 of this post

6. Conclusions

A bit short of a post this one, but it will have to do. We have laid the groundwork for clustering documents with order reducing transformations. Getting into the details and results will make this too long. We will get to that in the next post and conclude this series.