Classification hinges on the notion of similarity. This similarity can be as simple as a categorical feature value such as the color or shape of the objects we are classifying, or a more complex function of all categorical and/or continuous feature values that these objects possess. Documents can be classified as well using their quantifiable attributes such as size, file extension etc… Easy! But unfortunately it is the meaning/import of the text contained in the document is what we are usually interested in for classification.
The ingredients of text are words (and throw in punctuation as well) and the meaning of a text snippet is not a deterministic function of these constituents. We know that the same set of words but in a different order, or simply with different punctuation can convey different meanings. This level of sophistication in understanding text is beyond the reach of algorithms to date. Short of that, there are a few ways to massage text to make it amenable for analysis by algorithms. Documents and words need to be transformed into numbers/vectors that hopefully retain and reflect the relationships we know to exist among the original words and documents. That is a tall order for sure but there has been good progress on this starting with the decades old Vector Space Model (VSM) approach, and some exciting new entrants in this decade based on Word-Embedding approaches. The VSM approach turns documents into numerical vectors whereas the word-embedding approaches turn individual words into numerical vectors.
In this post we compare and contrast the use of document vectors with and without word embeddings for measuring similarity. We lay the groundwork for using word embeddings (pre-trained or custom-built) for text classification that we take up in the next post. Let us start with quick overview of document and word vectors and motivational examples around how they measure and preserve (or not!) the notion of similarity as we understand it to be.
1. Document Vectors and Similarity
In the VSM approach a document is represented as a vector in word space. An element in the vector is a measure (simple frequency count, normalized count, tf-idf, etc..) of the importance of the corresponding word for that document. We have gone over the mechanics of this in great detail and the rich analysis that this approach makes possible in our earlier posts – Stacks of Documents and Bags of Words and Reduced Order Models for Documents.
If two documents contain nearly the same distribution of words, the vectors they give rise to in the word space would be more parallel than otherwise. So the cosine between the two vectors would be closer to 1. Making the assumption that two documents with a similar distribution of words are similar (which we know to be an inexact statement!) the VSM approach takes cosine of the document vectors as the measure of their similarity. Clearly documents that do not share many words would be considered dissimilar in this model – once again an inexact conclusion to make. Let us look at few examples so we are clear about this.
1.1 Example 1 (Document Vectors)
Take the following three documents in a 7-dimensional word space:
- Word Space: [‘avoid’, ‘capital’, ‘france’, ‘japan’, ‘letters’, ‘paris’, ‘tokyo’]
- Doc1: Tokyo is the capital of Japan => d1 = [0, 1, 0, 1, 0, 0, 1]
- Doc2: Paris is the capital of France => d2 = [0, 1, 1, 0, 0, 1, 0]
- Doc3: Avoid capital letters => d3 = [1, 1, 0, 0, 1, 0, 0]
A simple count based VSM vector representation of each document is shown above as well. The cosine similarity between any pair of these vectors is equal to (0 + 1*1 + 0 + 0 + 0 + 0 + 0) / (30.5 * 30.5) = 1/3.0. The math is all correct but we would have liked to have gotten higher similarity between Doc1 & Doc2 so that we could put them together in a geography bucket while placing the third somewhere else. But that is the nature of bag-of-words approach to documents. Let us move on to an another example.
1.2. Example 2 (Document Vectors)
Take an another triplet of documents spanned by a 6-dimensional word space:
- Word Space: [‘decent’, ‘good’, ‘honest’, ‘lies’, ‘person’, ‘tell’]
- Doc1: Be honest and decent => d1 = [1, 0, 1, 0, 0, 0]
- Doc2: Be a good person => d2 = [0, 1, 0, 0, 1, 0]
- Doc3: Tell lies => d3 = [0, 0, 0, 1, 0, 1]
The documents do not share any words so their dot products are all zero, indicating that they are all dissimilar. But again we would have hoped to have gotten Doc1 & Doc2 to be more similar with either being more dissimilar to Doc3.
The upshot from the examples here is that the bag-of-words based document vectors for assessing similarity and thus classification thereof can be misleading.
2. Word Vectors and Similarity
Over the past five years or so there has been a burst of activity in coming up numerical vectors (of arbitrary length p = 50, 200, 300 etc…) for individual words. The reasons are centered around the availability of cheaper and faster computers and the desire to apply the newly popular & competitive deep neural nets for NLP tasks. Word-embedding based approaches have given rise to tools such as Word2Vec, Glove, and FastText that are in wide use now-a-days.
The word vectors are obtained by training the algorithm against a corpus of text data. At the end of training, each word in the corpus learns to be a numerical vector of length p chosen at the time of training. This p is much, much smaller than the total number n of unique words in the corpus, i.e. p << n. This vector thus represents a linear map/projection from original n-long 1-hot word vector, to the much smaller p-long dense vector in p-dimensional fake-word-space. The reason we say fake is that these p-dimensions do not have any interpretable physical meaning. They are simply a mathematical construct. Somewhat like SVD but not exactly. One might think that increasing p may yield better quality representations of the words in the lower dimensional manifold. Not quite unfortunately. So, there we go – a bit of voodoo and the alleged alchemy at work.
The authors of these tools have applied them against vast amounts of text such as google news, wikipedia dump, common crawl etc… to come up with their versions of numerical vectors for words they found in those corpora. Why vast amounts of text? The idea is that these word vectors would hopefully be universal. What do we mean by that? That, we can replace the words in our documents with the numerical vectors that they have published. That is, they hope that their word vectors have universal validity – that is, no matter where and in which context that word appears in any document, that word can be replaced by the vector they have published
By exposing the algorithms to vast amounts of text, they hope that each word has seen enough variety of contexts and its numerical vector thus has absorbed in some average sense the meaning of the word and its relation to others in the optimization process
How universal are these word vectors?
The meaning and limitations of these universal word embeddings has to be clearly understood however.
- First, the numerical vector obtained for a word is a function of both the algorithm and the text corpus the algorithm was applied on to derive that vector.
- Second, do not mix up vectors across algorithms – even if they have been trained on the same corpus. That is, do not use Glove vectors for some words, and Word2Vec vectors for other words in your documents. These vectors are different and do not embed the relations they learn in the same way.
- Third, do not mix up these vectors across corpora – even if the same algorithm is used. That is, do not use a vector obtained by training on say movie reviews for one word, and a vector obtained by training on say political news stories for an another word in your document.
The table below summarizes the above assessments. Consider two words – ‘good‘ and ‘decent‘. Each has a pre-trained numerical vector published by Word2Vec (trained on Google News), Glove (trained on Wikipedia), and FastText (trained on common-crawl). Plus, I have custom vectors by training the same algorithms against the twenty-news group dataset that is programatically available from SciKit pages. The training is done with the Gensim package.
The values in the table show the cosine similarity between these two word vectors obtained in five different ways. Given that the words are similar, we would have expected scores to be closer to 1 if the word vectors are totally universal. But we see that this is the case only when both the vectors have been derived using the same algorithm trained against the same text corpus.
| Algorithm/Corpus | Word2Vec |
Glove |
FastText | Word2Vec | FastText |
|
Word2Vec |
0.684 | 0.006 | 0.007 | -0.044 | -0.081 |
|
Glove |
0.066 | 0.618 | 0.012 | -0.007 | 0.037 |
| FastText | 0.044 | 0.041 | 0.798 | -0.098 | 0.087 |
| Word2Vec | 0.075 | 0.014 | -0.081 | 0.668 | 0.012 |
| FastText | -0.05 | -0.069 | 0.07 | 0.042 | 0.631 |
| Table 1. The values represent the cosine similarity between the two numerical vectors for the words ‘good’ and ‘decent’. The diagonal cells represent the case when both vectors have been obtained with the same algorithm, trained on the same corpus. Hence they show the expected similarity scores while the rest are randomly close to 0. | |||||
The point here is that the word vectors obtained by training an algorithm on a text corpus are a package. These vectors have embedded the relations that they have come across between the words while training. Collectively these vectors loosely reflect the relationships between the words as contained in the corpus trained on, and as taught by the algorithm. We are not forced to use these pre-trained vectors of course as there are packages such as Gensim that can generate custom word vectors for any text corpus at hand.
3. Document Vectors with Word Embeddings
In general the number of unique words in a given document is a small, small fraction of the total number of unique words in the corpus. So the document vectors are sparse with many more zeros than non-zeros. This is a problem especially for neural nets where the number of input layer neurons is the size of the incoming vector. This is why the embedded word vectors have become popular.
The length of the trained word vectors p is in general much, much smaller than the size of the corpus word space. So the document vectors where the words are replaced with their lower dimensional vectors are much shorter – thus offering computational advantages. For example, the twenty-news document repository has over 60,000 unique words. If we use 300-dimensional word vectors (i.e. p = 300) for each word, we can cut down the number of input neurons by a factor of 200, making it much more competitive to use them in large NLP tasks.
3.1 Sparse to Dense Document Vectors
If every word in a document has a known representation in the same p-dimensional space, then the bag-of-words document vector can be represented as a vector in that same p-dimensional space. We are simply combining the bag-of-words approach with word embeddings to come up with lower dimensional, dense representations of documents. Let us take the example 1.2 from earlier where we now also have a px1 vector representation for each of the six words ‘decent’, ‘good’, ‘honest’, ‘lies’, ‘person’, ‘tell’ making up the corpus vocabulary. The original 6-dimensional document vector d1 can be rewritten in p-space as a px1 vector d*1
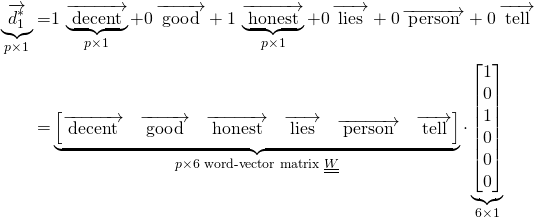
For the general case with m documents and n words we can directly extend the above. First we obtain word vectors for each of these n words, thus giving us the pxn word-vector matrix W. The ith document with a vector representation di in the standard n-word space is transformed to the vector d*i in the fake p-word-space with:
(1) 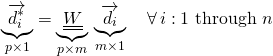
While it is a computational advantage to have shorter document vectors, we need to make sure that the documents have not lost their meaning and relationships in the process. Let us rework the examples 1.1 and 1.2 with these word-emdeddings in place and see what we get.
3.2 Example 1.1 (Document Vectors with Word Embeddings)
Table 2 below shows the similarity for the same documents in example 1.1 but now computed with document vectors with word embeddings.
- Doc1: Tokyo is the capital of Japan => d1 = [0, 1, 0, 1, 0, 0, 1]
- Doc2: Paris is the capital of France => d2 = [0, 1, 1, 0, 0, 1, 0]
- Doc3: Avoid capital letters => d3 = [1, 1, 0, 0, 1, 0, 0]
| Algorithm / Corpus | Doc1 & Doc2 | Doc2 & Doc3 | Doc3 & Doc1 |
| Document Vectors
with No word embedding
|
0.333 | 0.333 | 0.333 |
| Word2Vec | 0.665 | 0.306 | 0.307 |
| Glove | 0.578 | 0.564 | 0.514 |
| FastText | 0.691 | 0.536 | 0.438 |
|
Table 2. The pure document vectors yield that the three documents are similar. Incorporating word embeddings in the document vectors improves the prediction by yielding Doc1 & Doc2 to be more similar to each other, while being dissimilar to Doc3. |
|||
While the results are by no means perfect there is some improvement in the similarity score between Doc1 & Doc2. The skip-gram based Word2Vec algorithm with negative sampling (SGNS) actually comes up with lower similarities (compared to pure document vector based similarity) between Doc2 & Doc3 and Doc3 & Doc1. But we should not read too much into it however based on one test. Let us look at the other example.
3.3 Example 1.2 (Document Vectors with Word Embeddings)
Table 3 repeats the above exercise for the documents in example 1.2, where the pure document vector based approach yielded zero similarity between the 3 pairs of documents.
- Doc1: Be honest and decent => d1 = [1, 0, 1, 0, 0, 0]
- Doc2: Be a good person => d2 = [0, 1, 0, 0, 1, 0]
- Doc3: Tell lies => d3 = [0, 0, 0, 1, 0, 1]
| Algorithm / Corpus | Doc1 & Doc2 | Doc2 & Doc3 | Doc3 & Doc1 |
| Document Vectors
with No word embedding
|
0 | 0 | 0 |
| Word2Vec | 0.562 | 0.235 | 0.248 |
| Glove | 0.631 | 0.464 | 0.3 |
| FastText | 0.744 | 0.481 | 0.438 |
| Table 3. The pure document vectors yield that the three documents are dissimilar. Incorporating word embeddings in the document vectors improves the prediction by yielding Doc1 & Doc2 to be more similar while being dissimilar to Doc3. |
|||
Once again while the results are not perfect there is definite improvement. Doc1 & Doc2 show much higher similarity in every scheme, compared to the similarities obtained between Doc2 & Doc3 and Doc3 & Doc1.
4. Conclusions
With that we conclude this post. As stated in the introduction, we have laid out the groundwork for applying word embeddings in conjunction with VSM based document vectors. Specifically, we have:
- computed similarity of documents as numerical vectors obtained via bag-of-words approach
- computed similarity between words as numerical vectors obtained via different word-embedding algorithms, both pre-trained & trained on custom text corpus
- examined the limitations of the universality of the word-embeddings
- computed similarity between document vectors with word-embeddings
All this in preparation towards using these reduced order, words-embedded document vectors in classification exercises. We will take it up in the next post.
Pingback: Predicting ICU Readmission from Discharge Notes: Important Phrases - TechMintz
Pingback: Predicting ICU Readmission from Discharge Notes: Significant Terms – Data Science Austria