Naive Bayes Classifier: Part 2. Characterization and Evaluation

      No Comments on Naive Bayes Classifier: Part 2. Characterization and Evaluation

Closed-form solutions are sweet. No hand-wringing/waving required to make a point. Given the assumptions, the model predictions are exact so we can readily evaluate the impact of assumptions. And, we get the means to evaluate alternate (e.g. numerical) approaches applied to these same limiting cases with the exact solution. We are of course talking about the previous post where we obtained closed-form solutions to the Naive Bayes predicted decision boundaries when the true decision boundary was a known linear or nonlinear form. As there is good bit of ground to cover we will start in earnest with the “Next Steps” we outlined in the previous post. Please review it if needed as there is little room for repetition in a 2000+ word article as my posts tend to be. Somewhat of a longer post this one actually, but mainly because of diagrams and simulation results so should not be too bad.

1. The Confusion Matrix

For our 2-class (C1 and “Not C1” – or C2 as we used to call it in the previous post) and 2-feature ([x, y]) situation a nice way to characterize the performance of any classifier is to compute the confusion matrix shown in Figure 1 below. The true and predicted boundaries intersect and split the feature space into four zones. The data points in these zones have either been correctly (i.e. True) or incorrectly (i.e. False) identified as belonging (i.e. Positive) to C1 or not (i.e Negative). For example the top-right corner zone is marked as False Negative, as the prediction falsely classified it as  ‘Not C1‘ . The naming of the other zones follows likewise.

Figure 1. Evaluating the confusion matrix in the assignment of a class C1  to a data point. The areas of intersection FP and FN are the key variables determining the quality of the classifier

The areas of intersection FP and FN and any metrics computed thereof yield significant insight into the effectiveness of the classifier. For example, a highly specific classifier for C1 will never place a true ‘not C1‘ data point in a ‘C1‘ zone. Likewise if the classifier is highly sensitive to C1, it will never place a true C1 in ‘not C1‘ zone. The overall accuracy of the classifier would of course be the fraction of correct predictions. All this leads to the following definitions that are commonly employed.

(1)   \begin{equation*} \text{Sensitivity } = \frac{TP}{TP + FN} \quad \text{Specificity } = \frac{TN}{TN + FP} \quad \text{Accuracy} = \frac{TP + TN}{TP + TN + FP + FN} \end{equation*}

Each classification exercise yields a value for each of these metrics. Running a series of such exercises and collecting these metrics from each run we can characterize how good the classifier is for data in this feature space. High sensitivity (small FN zone) & high specificity (small FP zone) are naturally the ideal characteristics for a classifier.

2. The Areas of Intersection

With the prelims out of the way we are ready to quantify how well the Naive Bayes classifier did for the linear and nonlinear boundaries we considered in the previous post. As shown in Figure 2 below, each value of k splits the feature space between A1 and A2, while A1 + A2 stays constant. The predicted boundary is a function of this parameter k naturally and each such predicted boundary yields a value for FN, and FP the areas of intersection we are interested in.

Figure 2. As the point P moves, the feature space gets split between the classes. FP and FN are the areas of interest that meet at the intersection point of the true and predicted boundaries. (A) Point P moves vertically from 0 through b. The true and predicted boundaries always intersect at (a/2, k/2) (B) Point P moves horizontally from 0 through a . The intersection point x* for the true and predicted boundaries is a root of the quadratic given in Equation 6.

In case of the nonlinear parabolic boundary we work with y = kx2 rather than y = x2 as we had in the previous post.  Deriving the updated decision boundary is a straightforward application of the same geometric procedure detailed earlier. We simply write down the results for both the linear and parabolic cases here for easy reference. yp stands for the predicted boundary in the following and we use yt for the true boundary.

(2)   \begin{equation*} \text{Linear: } \, \frac{k}{y_p} = 1 + \frac{1}{2b -k} \left[ \frac{ab}{x} - k \right] \end{equation*}

(3)   \begin{equation*} \text{Parabolic: } \, \frac{a}{\sqrt{y_p}} = \frac{1}{\sqrt{k}} + \frac{1}{\sqrt{k}} \left[ \frac{3a}{2\sqrt{b/k}} - 1\right] \left[ \frac{b}{kx^2} - 1 \right] \end{equation*}

Figure 3. Varying k is a means to change the relative class sizes while holding the total size constant. In all the cases above a = b = 1.0, so A1 + A2 = 1.0. When one of the class sizes goes to zero i.e. A1/A2 → ∞ for the linear case, and A1/A2 → 0 for the parabolic case we expect better predictions in either case as indicated by vanishing FP and FN. (A) For linear case, naive bayes prediction is exact, i.e FP = FN = 0 for A1/A2 = 1 (B) For the nonlinear case has FN = 0, but FP is at maximum when A1/A2 = 2.

Figure 3 illustrates the dynamic interplay and tradeoff between FP and FN as k is varied in either case. The areas of intersection FP and FN are what we are after and they can be integrated for directly as we have explicit equations for yp and yt.

2.1 FP and FN for the linear case

In the linear case we know that the true and predicted boundaries intersect at the point (a/2, k/2).

(4)   \begin{equation*} FN = \int_{0}^{a/2} (y_p - y_t) dx \quad FP = \int_{a/2}^{a} (y_t - y_p) dx \end{equation*}

Plugging in yt = kx/a and yp from Equation 2, integrating and simplifying we get:

(5)   \begin{align*} FN = & \frac{ak(2b-k)}{4(b-k)} - \frac{ak}{8} + \frac{abk(2b-k)}{4(b-k)^2} \, \ln{\frac{b}{2b-k}} \\ FP = & \frac{3ak}{8} - \frac{ak(2b-k)}{4(b-k)} + \frac{abk(2b-k)}{4(b-k)^2} \ln{\frac{3b - 2k}{2b - k}} \end{align*}

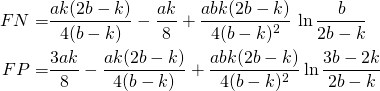
2.2 FP and FN for the parabolic case

The point of intersection here is the solution to the equation yp= k x2 where yp is given by Equation 3. Unfortunately there is no explict solution but the whole thing simplifies to a quadratic that needs to be solved for a root that makes sense.

(6)   \begin{align*} \text{Solve for } x \, : & \left(4 \sqrt{bk} - 3ak \right) \, x^2 - 2a\sqrt{bk} \, x + b \left( 3a - 2\sqrt{b/k} \right) = 0 \\ \text{Pick the root: } & x^* > 0 \, \text { and } x^* < \sqrt{b/k} \end{align*}

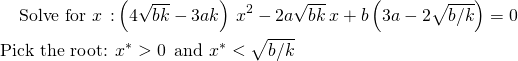
Referring to Figure 2B, the areas FP and FN are obtained as

(7)   \begin{equation*} FP = \int_{0}^{x^*} (y_t - y_p) dx \quad FN = \int_{x^*}^{\sqrt{b/k}} (\text{min }(y_p, b) - \text{min } (y_t, b)) dx \end{equation*}

The integrand and the limits are known exactly so the integral can be precisely evaluated numerically with a code snippet such as:

3. The Characteristics

With the means to get FP and FN for any k we are ready to evaluate the classifier with respect to its sensitivity, specificity etc… measures we went over in Section 1. TP and TN follow directly from the geometry.

(8)   \begin{equation*} TP = A_1 - FN \quad \text{and} \quad TN = A_2 - FP \end{equation*}

Figure 4 shows the intersection areas and the obtained metrics thereof as a function of A1/A2 . FP and FN areas are small fractions of the overall areas, and the accuracy is excellent. There is no question that metrics are quite good in both cases even while the linear case seems to have an edge. The range of A1/A2  in these results is somewhat constrained (0 → 2 in the parabolic case, and 1 → ∞ in the linear case) in both cases due to the design of the derived solutions.

Figure 4. In all the cases above a = b = 1.0, so A1 + A2 = 1.0. (A) Both the intersection areas FP, FN go to zero for the linear case when A1/A2 = 1 and when A1/A2 → ∞ as expected. Only FN is zero in the parabolic case when A1/A2 = 2 confirming our assessment from Figure 3. (B) The naive bayes classifier is more sensitive than specific in either case.

The observation in Figure 4B that sensitivity, specificity and accuracy go through a single point is no fluke. When sensitivity and specificity are equal,

    \[ \frac{TP}{TP + FN} = \frac{TN}{TN + FP} \equiv \frac{TP + TN}{TP + FN + TN + FP} \]

where the last expression is the definition of accuracy.

4. Numerical Simulations with SciKit

SciKit has excellent implementations of algorithms including naive bayes for classification. Gaussian Naive Bayes approximates a gaussian distribution from the training data to estimate P(x|C1) and P(y|C1) for new data point  x,y. This is fine when this new data point x,y is away from the decision boundary but will clearly have some error otherwise. What is the consequence of this error on classification is the question we seek to explore here with a few numerical simulations. Further, we apply a couple of competing classification techniques namely Logistic Regression and MLPClassifier, again as implemented in SciKit. Analysis of assumptions built into these other techniques is the subject matter for a different post. Here we simply use them – SciKit makes it very easy to try things out.

Generating training and test data is a breeze, as we know the exact decision boundary. Lines 7 and 10 in the code snippet below read in the data.

We use default values for the parameters for the most part for the three classifiers initialized in Lines 14-16. The MLPClassifier uses 100 neurons and one hidden layer by default. One hidden layer is fine, but given that we only have 2 input neurons (one for x and the other for y), using 100 hidden neurons is an overkill. We pick 4, we could likely do with even less. Line 20 trains the model, and in Line 23 we obtain the confusion matrix. All the other metrics can be computed off of that of course.

4.1 Error from the Gaussian Approximation in SciKit

Figure 5. In all the cases above a = b = 1.0 so A1 + A2 = 1.0. MLP uses a single hidden layer with 4 neurons. (A) & (C)) The mispredictions from gaussian naive bayes overlap and extend beyond the analytic results (B) Both logistic regression and MLP have essentially no mispredictions in the linear case (D) Logistic regression (in red) does worse than MLP for the nonlinear case.

Figures 5A and 5C show the results from SciKit’s gaussian naive bayes simulation for the linear case with k = 0.6 (i.e. A1/A2 = 2.33). The misprediction zones in red are larger compared to the same obtained with analytic naive bayes predictions. Logistic regression is known to be a linear classifier so the near perfect prediction in Figure 5B is to be expected. MLP is of course the best of the lot in all cases even with just 4 neurons in a single hidden layer. But we shall see later that this happy scenario does not hold for boundaries with more severe nonlinearities.

4.2 Classification Metrics

Figure 6 compares the performance of the three classifiers over a number of simulations where the ratio A1/A2 is varied while holding A1 + A2 at unity. This is much like Figure 4 where we compared analytic naive bayes predictions against the truth. A few easy observations are as follows.

Figure 6. In all the cases above a = b = 1.0, so A1 + A2 = 1.0. All three classifiers can be considered quite good even while MLP does beat out the rest in general.

  • Naive bayes has the largest error zones (FP and FN). FP for logistic regression increases with A1/A2 even in the linear case. Given that logistic regression is a linear classifier, this will require some further analysis as to why.
  • In terms of the total area of mischaracterization (i.e. FP + FN) we see that MLP, logistic regression, and naive bayes are in the order of decreasing excellence.
  • Depending on what is being demanded one may opt for a classifier that excels at that criteria. For example MLP is excellent here for specificity.

5. Are Neural Nets Better at Classification?

From the results in Sections 3 and 4, it would seem that neural networks are better at classification of data with linear or nonlinear separation boundaries. But such a generalization would likely be wrong. When we know the truth as is the case here, we can monkey with the number of hidden layers, the number of neurons within, activation functions etc… to get better matches with that truth. But that result may not have a general validity beyond the scope of that specific exercise. To see this in practice let us consider the case of a sine wave as the separation boundary and attempt to classify with the same three schemes.

(9)   \begin{equation*} y = \frac{b}{2} \left[ 1 + \sin \left( \frac{2 \pi k x}{a} \right) \right] \end{equation*}

As k increases, the feature space gets split into more and more number of non-contiguous zones for the classes, and classification gets harder. The mechanics of obtaining the classification results with SciKit are the same as in Section 4 so we go directly to the results.

Figures 7A plots the magnitudes of the areas of intersection as the number of non-contiguous zones is varied by varying k. Clearly MLP is no better for any k when we use a single hidden layer. MLP. FP and FP together take up about 20-30% of the total area, so there is that much data that would be incorrectly classified. This is reflected in the smaller specificity values in Figure 7B. With 6 hidden layers MLP has much smaller error zones for all k values, and thereby a much better specificity as seen in Figure 7B.

Figure 7. The upshot from the results here is that MLP can do better but careful experimentation is required before generalizing the applicability of the model. When k = 4, in Equation 9, there would be 4 non-contiguous zones for the two classes. (A) MLP with a single hidden layer yields no improvement over naive bayes or logistic regression for any k. Six hidden layers with ten neurons each yields better classification but there could be other combinations that can do equally well or better. (B) Much better specificity with 6 hidden layers for all values of k (C) – (E): Increasing the number of layers is not guaranteed to improve performance for MLP. It starts to get better as we add more hidden layers but worsens after 6 layers.

Figures 7C – 7E show the error zones obtained in all cases when k = 4. Error zones decrease as the hidden layers are increased, yielding the best classification for 6 layers. But unfortunately it does worse with 7 layers, somewhat unexpected… the alleged alchemy at play. There is clearly more going on here that requires deeper analysis.

6. Next Steps

With that we close this somewhat long but straightforward post. For the linear and parabolic separation boundaries we have shown that all three classifiers tested here were quite good, with MLP edging out logistic regression and naive bayes. The out performance of MLP is interesting but there is no clear understanding at this time as to how exactly it manages to do better. MLP can likely work well for more severe nonlinearities but careful experimentation may be required for generalizing the obtained results. Nevertheless, the results here are encouraging enough that we would like to try out neural nets for text classification problems in future posts.

Leave a Reply